Workflow

In this section you will learn how to create synthetic single molecule videos and trajectories. Exported data can be used for result validation, algorithm testing or external illustration.

The procedure includes four steps:

  1. Create a simulation-based project
  2. Generate random FRET state sequences
  3. Create intensity trajectories and images
  4. Validate and export data

Create a simulation-based project

The first step in simulating data is to create a new simulation-based project.

After the project creation is completed, it is recommended to save it to a .mash file that should regularly be overwritten in order to keep traceability and access to the results.

To create a new simulation-based project:

  1. Open the experiment settings window by pressing New project in the project management area and selecting simulate data.

  2. Name your project and define the plot colors by configuring tab Divers. If necessary, modify settings any time after project creation.

  3. Finalize the creation of your project by pressing Save; the experiment settings window now closes and the interface switches to module Simulation.

  4. Save modifications to a .mash file by pressing Save project in the project management area.

Generate random FRET state sequences

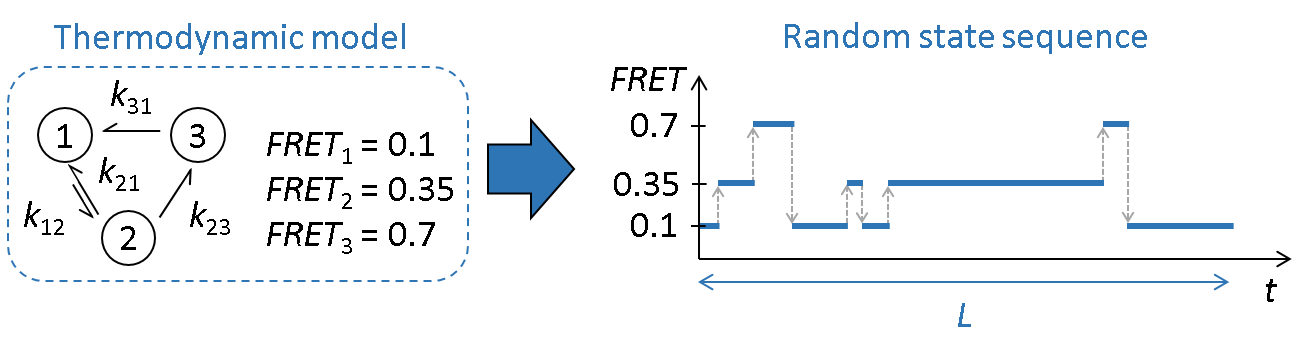
A FRET state sequence is the ideal FRET trajectory of a single molecule. It consists in a succession of plateaus dwelling at a particular state \(j\) with value \(FRET_j\) before transiting to the next state \(j'\) with value \(FRET_{j'}\).

In Simulation, sequences are started by randomly drawing a first state using the vector of normalized initial state probabilities \(\boldsymbol{\pi}\) such as:

\[\boldsymbol{\pi} = \begin{bmatrix} \pi_1 \\ \pi_2 \\ \vdots \\ \pi_n \end{bmatrix} \quad \mathrm{and} \quad \sum_j \pi_j = 1\]

with \(\pi_j\) the probability to start a chain in state \(j\).

The duration in the current state \(\Delta t\) given in nb. of time steps, is randomly drawn from the exponential dwell time distribution with scale parameter \(\tau_j\), defined as:

\[\Delta t_j \sim \mathrm{Exp}\!\left(\frac{1}{\tau_j} \right )\]

\(\tau_j\) is called the lifetime of state \(j\) and is given in nb. of time steps.

The advantage of random dwell time simulation over time-step simulation is that it gives access to the exact time spent in each state, which allows us to calculate the time-averaged contribution of state values during transitions.

The state sequence is then elongated by randomly drawing the next state \(j'\) using the exit distribution \(\boldsymbol{w}_j\) of the current state \(j\), defined as:

\[\boldsymbol{w}_j = \begin{bmatrix} w_{j1} & w_{j2} & \cdots & w_{jn} \end{bmatrix} \quad \mathrm{and} \quad \sum_{j'} w_{jj'} = 1\]

where \(w_{jj'}\) is the probability of transitioning to state \(j'\) given that the system leaves state \(j\), which implies that \(w_{jj'}=0\) for \(j=j'\).

The operation is repeated until the sequence length reaches the observation time and the number of sequences equals the number of molecules \(N\). The observation time is limited by the video length \(L\) but can be randomly drawn from an exponential distribution to mimick photobleaching of donor fluorophore:

\[L_n = \mathrm{min}\!\left( X, L\right)\]

where:

\[X \sim \mathrm{Exp}\!\left( \frac{1}{\tau_{\mathrm{bleach}}} \right)\]

where \(L_n\) is the observation time until donor photobleaching for molecule \(n\) and \(\tau_{\mathrm{bleach}}\) is the average time until donor photobleaching.

Molecule heterogeneity in FRET values can be induced by randomly drawing a \(FRET_{j,n}\) value for state \(j\) and molecule \(n\) from a Gaussian distribution such as:

\[FRET_{j,n} \sim \mathcal{N}\!\left( FRET_j,\, w_{FRET,j} \right)\]

Where \(w_{FRET,j}\) is strictly positive.

FRET state sequence

Initial state probabilities

Considering a population of unsynchronized molecules with stationary state transition kinetics, the probability \(\pi_j\) is the stationary probability, i.e., the probability of finding a molecule in state \(j\) at a random time during the process. It is obtained by solving the equation system:

\[\boldsymbol{\pi} = \boldsymbol{\pi} \boldsymbol{\mathrm{P}}\]

with \(\sum_j \pi_j = 1\), and where \(\boldsymbol{\mathrm{P}}\) is the transition probability matrix described as:

\[\boldsymbol{\mathrm{P}} = \begin{bmatrix} p_{11} & p_{12} & \cdots & p_{1n} \\ p_{21} & p_{22} & \cdots & p_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ p_{n1} & p_{n2} & \cdots & p_{nn} \end{bmatrix}\]

and obtained from the transition rate constants as:

\[p_{jj'} = \begin{cases} t_{\mathrm{exp}} k_{jj'}, & j \neq j', \\ 1-t_{\mathrm{exp}} \sum_{i \neq j} k_{ji}, & j = j' \end{cases}\]

where \(k_{jj'}\) is the transition rate constant governing state transition \(j\) to \(j'\) given in second-1 and \(t_{\mathrm{exp}}\) is the sampling time of the trajectory given in second.

Solving the equation comes down to finding the eigenvector of \(\boldsymbol{\mathrm{P}}\) associated with the eigenvalue 1 and normalizing it by its sum.

This approach is like segmenting an infinitely long chain at a random position. Therefore, it is only valid for chains that complete their cycles within an observation time, meaning that all states communicate and there are no irreversible transitions such as kinetic traps, parallel sub-populations, or other irreversible changes in folding dynamics. For such limiting cases, initial state probabilities must be pre-defined; see Remarks for details.

If no initial state probabilities are pre-defined, they are approximated from state lifetimes as:

\[\pi_j = \frac{\tau_j}{\sum_{i=1}^n \tau_i}\]

where \(\tau_j\) is the lifetime of state \(j\).

Finally, if the state lifetime is not provided via a presets file or computable from transition rate constants, as in the case of a kinetic trap, uniform initial state probabilities are used instead, with

\[\pi_j = \frac{1}{n}, \quad j = 1,\dots,n\]

State lifetimes

State lifetimes are calculated from transition rate constants, such that:

\[\tau_j = \frac{1}{t_{\mathrm{exp}} \sum_{j' \neq j} k_{jj'}}\]

where \(k_{jj'}\) is the transition rate constant governing state transition \(j\) to \(j'\) given in second-1 and \(t_{\mathrm{exp}}\) is the sampling time of the trajectory given in second. State lifetimes are given in nb. of time steps.

They can also be imported from presets files; see Remarks for details. In this case, they must be given together with exit probabilities and transition rate constants will be re-calculated as:

\[k_{jj'} = \frac{w{jj'}}{t_\mathrm{exp} \tau_j}\]

where \(\tau_j\) is the lifetime of state \(j\) given in nb. of time steps and \(t_\mathrm{exp}\) is the trajectory sampling time given in second.

Exit probabilities

The exit distribution \(\boldsymbol{w}_j\) of state \(j\) contains the transition probabilities conditional on leaving state \(j\).

Exit distributions are calculated from the transition rate constants such that:

\[\boldsymbol{w}_{jj'} = \frac{k_{jj'}}{\sum_{i \neq j}^n k_{ji}}\]

where \(k_{jj'}\) is the rate constant of state transition \(j\) to \(j'\).

Exit distributions can also be manually set via a preset parameter files. In this case, they must be given together with state lifetimes

To generate FRET state sequences:

  1. Set parameters:

    Video length
    Frame rate
    Number of molecules
    State configuration; see Remarks for more details
    Transition rates; see Remarks for more details
    Photobleaching

  2. Press Generate to generate random FRET state sequences,

  3. Generate new state sequences whenever one of the parameters is changed.

Create intensity trajectories and images

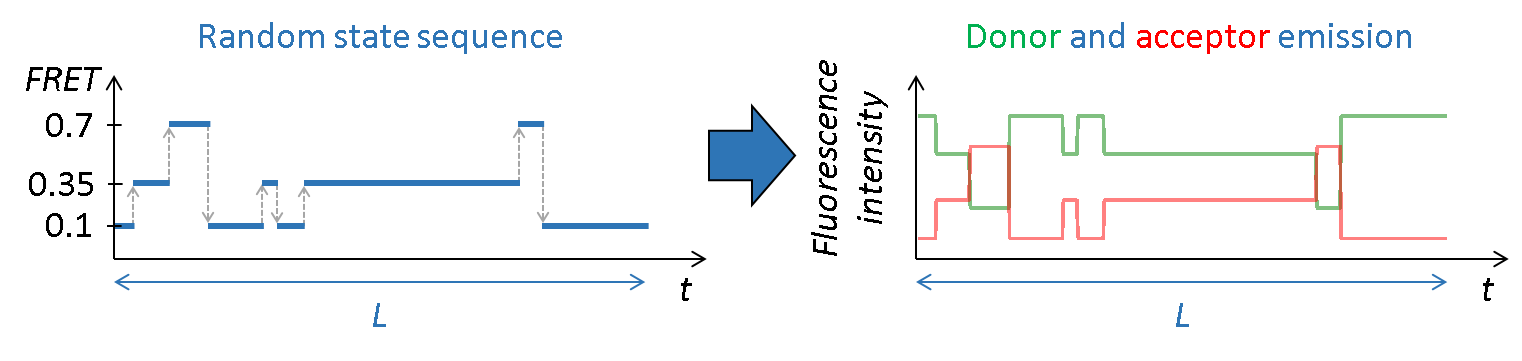
FRET state sequences \(FRET \left( t \right)\) are then converted into donor and acceptor fluorescence intensities using \(I_{\mathrm{tot}}\), the pure donor emission in the absence of acceptor with:

\[I_D\!\left( t \right) = I_{\mathrm{tot}} \left[ 1-FRET \!\left( t \right) \right]\] \[I_A\!\left( t \right) = I_{\mathrm{tot}} FRET\!\left( t \right)\]

Molecule heterogeneity in \(I_{\mathrm{tot}}\) values can be induced by randomly drawing an \(I_{\mathrm{tot},n}\) value for molecule \(n\) from a Gaussian distribution:

\[I_{\mathrm{tot},n} \sim \mathcal{N}\!\left( I_{\mathrm{tot}},\, w_{I,\mathrm{tot}} \right)\]

Where \(w_{I,\mathrm{tot}}\) is strictly positive.

Differences in donor and acceptor instrumental detection efficiencies and fluorophore quantum yields is induced here, by adjusting donor fluorescence intensities with the \(\gamma\) factor:

\[I_D^*\!\left( t \right) = \gamma I_D\!\left( t \right)\]

Imperfection in the detection and exitation paths of the instrument is simulated by adding channel-specific bleedthrough and direct excitation to the acceptor fluorescence intensity, such that:

\[I_A^*\!\left( t \right) = I_A\!\left( t \right) + Bt I_D^*\!\left( t \right) + DE I_{\mathrm{tot}}\]

where \(Bt\) is the bleedthrough coefficient of the donor into the acceptor detection path and \(DE\) is the direct excitation coefficient of the acceptor by the green laser.

Conversion to fluorescence

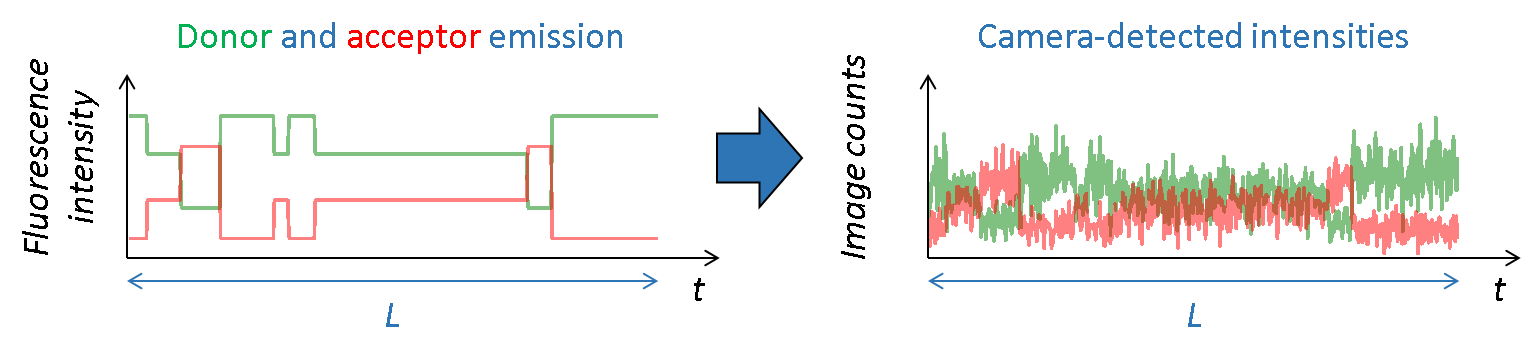
Channel-specific background intensities are added and Poissonian shot noise is simulated by randomly drawing a value from Poisson distributions:

\[I_A^{**}\!\left( t \right) \sim \mathrm{Pois}\!\left( I_A^*\!\left( t \right) + bg_A\!\left( t \right) \right)\] \[I_D^{**}\!\left( t \right) \sim \mathrm{Pois}\!\left( I_D^*\!\left( t \right) + bg_D\!\left( t \right) \right)\]

where \(bg_A\!\left( t \right)\) and \(bg_D\!\left( t \right)\) are background light contributions at time step \(t\) in donor and accpetor detection paths, respectively.

Final camera-detected intensity-time traces are obtained by randomly drawing values at each time step of the trajectory from the chosen noise disribution \(\mathrm{Cam}\):

\[I_A^{***}\!\left( t \right) \sim \mathrm{Cam}\!\left( I_A^{**}\!\left( t \right) \right)\]

In the specific case of Gaussian camera noise, shot noise is not simulated prior adding camera noise and values are directly randomly drawn from the Gaussian distribution

\[I_A^{***}\!\left( t \right) \sim \mathcal{N}\!\left( I_A^*\!\left( t \right) + bg_A\!\left( t \right),\, \sqrt{I_A^*\!\left( t \right) + bg_A\!\left( t \right)} \right)\] \[I_D^{***}\!\left( t \right) \sim \mathcal{N}\!\left( I_D^*\!\left( t \right) + bg_D\!\left( t \right),\, \sqrt{I_D^*\!\left( t \right) + bg_D\!\left( t \right)} \right)\]

see Camera SNR characteristics for more information.

Conversion to image counts

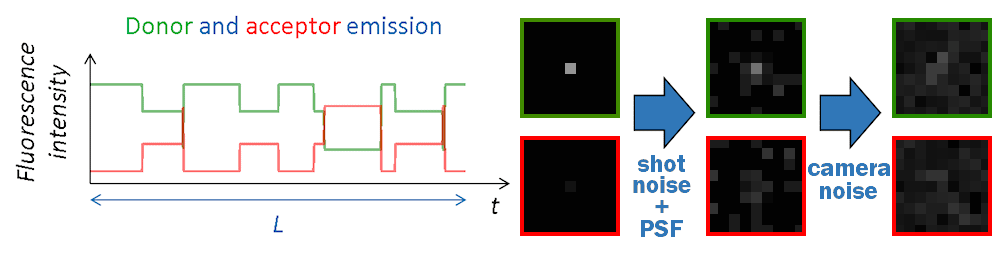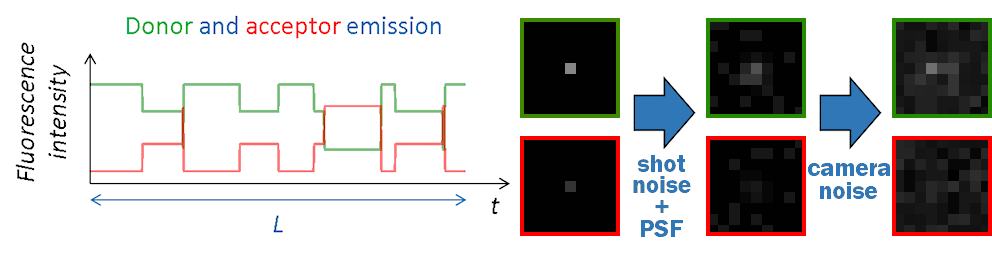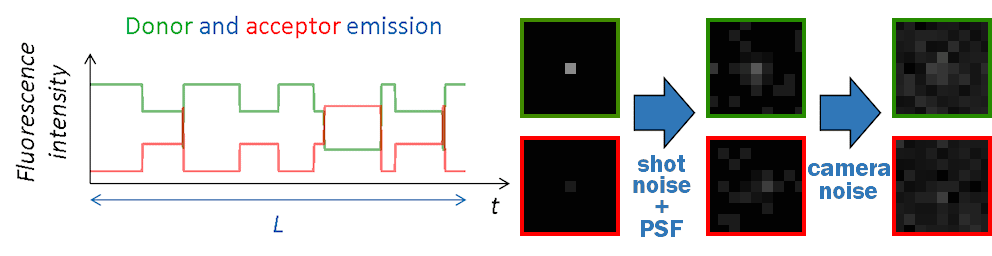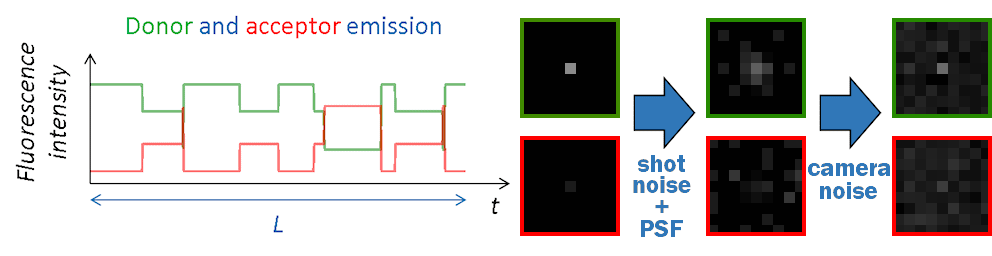
Images in the single molecule video (SMV) are created one by one, with the first image corresponding to the first time point in intensity-time traces.

Like in a 2-color FRET experiment, horizontal dimensions of the video are equally split into donor (left) and acceptor (right) channels. Single molecules are then spread randomly on the donor channel and translated into the acceptor channel.

At molecule coordinates, pixel values are set to donor or acceptor pure fluorescence intensities, including gamma factor and setup bias. All other sources of detected lights are then added as channel-specific background intensities that can be uniform, spatially distributed and/or dynamic in time.

Pixels are then convolved with channel-specific point spread functions to obtain realistic diffraction-limited images and uniform camera noise is added to all pixels to convert fluorescence intensities to camera-detected signal.

Building SMV

To create intensity trajectories and images:

  1. Set parameters:

    Video dimensions
    Pixel size
    Bit depth
    Camera SNR characteristics
    Molecule coordinates
    Donor emission
    Cross-talks
    Point spread functions
    Background

  2. Press Update to convert FRET state sequences into camera-detected intensity trajectories and images. The execution time can be long; see Remarks for details.

  3. Update intensity data whenever one of the parameters is changed.

Validate and export data

Simulated data and simulation parameters can be exported to various file formats. Intensities can be converted into photon counts or image counts before being written to files. When exporting the SMV, video frames are successively written in files until the video length is reached.

After export, even if no file was exported, simulated intensity-time traces and FRET state sequences are made immediately available in modules Trace processing, Histogram analysis and Transition analysis.

To validate and export data to files:

  1. Set parameters:

    File options
    Intensity units

  2. Press Export files to start writing files and refresh data in modules Trace processing, Histogram analysis and Transition analysis. The execution time can be long; see Remarks for details.

Remarks

To bypass the limitations of the user interface and (1), work with more than five states, (2), set pre-defined initial state probabilities and/or exit probabilities together with state lifetimes, or (3), set parameters for individual molecules to induce heterogeneity in the sample, simulation parameters can be loaded from external files; see Pre-set parameters for more information.

Updating intensity data and writing SMVs to files can be relatively time consuming depending on which camera characteristics are chosen; see Camera SNR characteristics for more information.